Personal solution to the book Quantum Computation and Quantum Information by Michael A. Nielsen & Isaac L. Chuang, chapter 4.
Currently under construction. Obviously won’t solve them all, but I’ll try my best. Open to valuable critics and better solutions.
S4.2 Single qubit operations
ex 4.2
method 1: use taylor expansion to check left and right are equal.
method 2: Since the matrix $A$ is involutory, it is non-defective and can be eigen-decomposed with $\pm 1$ eigenvalues. $$ A = P^{-1}SP $$ in which $S$ is a signature matrix (diagonal matrix with $\pm 1$ on diagonal). Then
$$ \exp(iAx)= P^{-1} \exp(iSx) P $$ For the part in the middle, $\exp(\pm ix)=\cos(x)\pm i\sin(x)$, $\exp(iSx)=\cos(x)I+i\sin(x)S$
$$\begin{align*} \exp(iAx) & = \cos(x)P^{-1}P+i\sin(x)P^{-1}SP \\ & = \cos(x)I + i\sin(x)A \end{align*} $$
ex 4.6
$$ R_{\hat{n}}(\theta) \equiv \exp (-i \theta \hat{n} \cdot \vec{\sigma} / 2)=\cos \left(\frac{\theta}{2}\right) I-i \sin \left(\frac{\theta}{2}\right)\left(n_{x} X+n_{y} Y+n_{z} Z\right) $$
First of all, it is obvoius that $R_{\hat n}(\theta)$ is a unitary, thus norm-preserving, which makes it qualified to be an rotation. Next we want to check the rotation axis is indeed $\hat{n}$, and the rotation angle is $\theta$ around that axis.
check rotation axis
The definition of $R_{\hat{n}}(\theta)$ involves both operators in bloch sphere: $I,X,Y,Z$, and coefficients in 3d cartesian coordiante: $n_x, n_y, n_z$. We can’t use it before we transform it into a valid operation in one of the two coordinate systems.
Since $\hat{n}$ is a unit vector, we can regard it as a state vector on the bloch sphere representing the state: $$ \ket{n} = \cos{\alpha\over2}\ket{0}+e^{i\phi}\sin{\alpha\over2}\ket{1} = \begin{pmatrix} \cos{\alpha\over2} \\ e^{i\phi}\sin{\alpha\over2} \end{pmatrix} $$
then its cartesian coordiante is
$$ \hat{n} = \begin{pmatrix} \sin{\alpha}\cos{\phi} \\ \sin{\alpha}\sin{\phi} \\ \cos{\alpha} \end{pmatrix} $$
with $n_x = \sin{\alpha}\cos{\phi}$, $n_y = \sin{\alpha}\sin{\phi}$ and $n_z = \cos{\alpha}$, we can get $$ R_{\hat{n}}(\theta) = \begin{bmatrix} \cos{\theta\over 2} - i\sin{\theta\over2}\cos{\alpha} & -i\sin{\theta\over 2}\sin{\alpha}\cdot e^{-i\phi} \\ -i\sin{\theta\over2}\sin{\alpha}\cdot e^{i\phi} & \cos{\theta\over 2} + i\sin{\theta\over2}\cos{\alpha} \end{bmatrix} $$
Then we do eigen-decoposition to check $\ket{n}$ is the rotation axis, the eigenvalue-eigenvector pairs are: $$\begin{align*} & e^{i{\theta\over2}},\quad \begin{pmatrix} \sin{\alpha\over2} \\ -e^{i\phi}\cos{\alpha\over2} \end{pmatrix} \\ & e^{-i{\theta\over2}},\quad \begin{pmatrix} \cos{\alpha\over2} \\ e^{i\phi}\sin{\alpha\over2} \end{pmatrix} \end{align*}$$
It is clear that $\ket{n}$ is one of the eigen-vector as we expected. The another eigenvector on the bloch sphere is in the opposite direction of $\ket{n}$ and is orthogonal to $\ket{n}$. We can name it $\ket{n_\perp}$.
check rotation angle
$\ket{n}$ and $\ket{n_\perp}$ form a basis in bloch sphere. Thus any state vector can be written in this basis. Let
$$ \ket{\lambda} = a\ket{n}+b\ket{n_\perp} $$
Then $$\begin{align*} R_{\hat{n}}(\theta)\ket{\lambda} & = \begin{bmatrix} e^{-i{\theta\over2}} & \\ & e^{i{\theta\over2}} \end{bmatrix}\begin{bmatrix} a \\ b \end{bmatrix} \\ & = e^{-i{\theta\over2}}\begin{bmatrix} 1 & \\ & e^{i{\theta}} \end{bmatrix}\begin{bmatrix} a \\ b \end{bmatrix} \end{align*}$$
In the eigenspace of $R_{\hat{n}}(\theta)$, $\ket{\lambda}$ gains a phase rotation of angle $\theta$ with a global phase $ e^{-i{\theta\over2}}$. In other words, $R_{\hat{n}}(\theta)$ rotate $\ket{\lambda}$ angle $\theta$ around axis $\hat{n}$.
ex 4.7
$$\begin{align*} XR_y(\theta)X & = X e^{-i\theta/2Y}X \\ & = X(\cos(\theta/2)I+i\sin(\theta/2)Y)X \\ & = \cos(\theta/2)X^2+i\sin(\theta/2)XYX \\ & = \cos(\theta/2)I-i\sin(\theta/2)Y \\ XR_y(\theta)X & = R_y(-\theta) \end{align*} $$
S4.3 Controlled operations
Summary
ex 4.20
Since
$$ H\otimes H = {1\over \sqrt 2} \begin{bmatrix}H & H \\ H & -H \end{bmatrix} $$
Due to the fact that $H$ is hermitian and unitary, $HH=HH^\dagger=I$. Also using identity: $HXH=Z$, we have
$$\begin{align*} H\otimes H\cdot CNOT01 \cdot H\otimes H & = {1\over2}\begin{bmatrix}H&H \\ H&-H\end{bmatrix}\begin{bmatrix}I \\ &X \end{bmatrix}\begin{bmatrix}H&H \\ H&-H\end{bmatrix} \\ & = \begin{bmatrix}1&0&0&0 \\ 0&0&0&1 \\ 0&0&1&0 \\ 0&1&0&0\end{bmatrix}\equiv CNOT10 \end{align*}$$
ex 4.21
Circuit on the left: $$\text{left} : C^2(U)=\begin{bmatrix}I \\ & I \\ & & I \\ & & & U \end{bmatrix}$$ Using $VV^\dagger=V^\dagger V=I$ and $V^2=U$ we have:
$$\begin{align*} \text{right} & : I\otimes \begin{bmatrix}I \\ & V\end{bmatrix} \cdot \begin{bmatrix}I \\ & X\end{bmatrix} \otimes I \cdot I\otimes \begin{bmatrix}I \\ & V^\dagger\end{bmatrix} \cdot \begin{bmatrix}I \\ & X\end{bmatrix} \otimes I \cdot \begin{bmatrix} I \\ & I \\ & & V \\ & & & V \end{bmatrix} \\ & = \begin{bmatrix} I \\ & I \\ & & I \\ & & & U \end{bmatrix} \end{align*}$$ $\text{left = right}$
ex 4.22
step1 - substitution
Use decomposition $U=e^{i\alpha}AXBXC$ to replace $c\text{-}V$ and $c\text{-}V^\dagger$ with correponding decompositions. Note that, if $V=e^{i\alpha}AXBXC$, then
$$V^\dagger=(e^{i\alpha}AXBXC)^\dagger=C^\dagger X B^\dagger XA^\dagger e^{-i\alpha}$$
By substituting $c\text{-}V$ and $c\text{-}V^\dagger$, we have

step2 - simplification
Use $AA^\dagger=C^\dagger C=I$ to simplify the circuit:

Furthur simplify the circuit using:
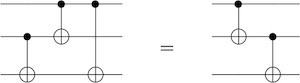
and
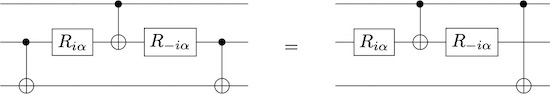
Result
The final design with 8 one-bit gates and 6 CNOTs for $C^2(U)$ is:
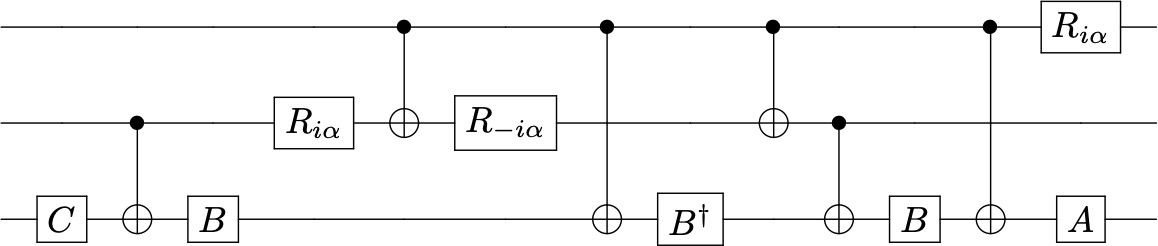
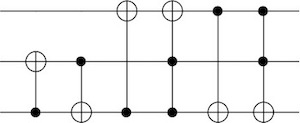
ex 4.27
S4.4 Measurement
S4.5 Universal quantum gates
ex 4.36
First two qubits represent x and last two qubits represent y
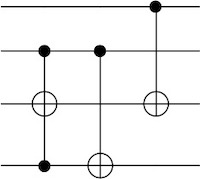
ex 4.40
By definition:
$$\begin{align*} E(R_{\hat n}(\alpha),R_{\hat n}(\alpha+\beta)) & = \max_{\ket\psi}{\Vert{(R_{\hat n}(\alpha)-R_{\hat n}(\alpha+\beta))\ket\psi}\Vert} \\ & = \max_{\ket\psi}{\Vert{(I-R_{\hat n}(\beta))R_{\hat n}(\alpha)\ket\psi}\Vert} \\ & = \max_{\ket\phi}{\Vert{(I-R_{\hat n}(\beta))\ket\phi}\Vert}, \quad \ket\phi=R_{\hat n}(\alpha)\ket\psi \\ \end{align*}$$
Geometrically, the maximum is acheived when $\ket \phi\perp\hat n$, then $R_{\hat n}(\beta)$ is a 2D rotation on a unit circle with angle $\beta/2$. The value of the maximum is the norm of the cord facing the $\beta/2$ angle. Thus:
$$E(R_{\hat n}(\alpha),R_{\hat n}(\alpha+\beta))=\max_{\ket\phi}{\Vert{(I-R_{\hat n}(\beta))\ket\phi}\Vert}=\vert{1-e^{i\beta/2}}\vert$$
ex 4.41
$$\begin{align*} \ket{00\psi} & \xrightarrow{H} {1\over2}(\ket{00}+\ket{01}+\ket{10}+\ket{11})\ket\psi \\ & \xrightarrow{Toffoli,S}{1\over2}(\ket{00}S\ket\psi+\ket{01}S\ket\psi+\ket{10}S\ket\psi+\ket{11}SX\ket\psi) \\ & \qquad= {1\over\sqrt{2}}\ket{0+}S\ket\psi+{1\over2}\ket{10}S\ket\psi+{1\over2}\ket{11}SX\ket\psi \\ & \xrightarrow{Toffoli} {1\over\sqrt{2}}\ket{0+}S\ket\psi+{1\over2}\ket{10}S\ket\psi+{1\over2}\ket{11}XSX\ket\psi\\ & \xrightarrow{H} {1\over\sqrt{2}}\ket{+0}S\ket\psi+{1\over2}\ket{-+}S\ket\psi+{1\over2}\ket{–}XSX\ket\psi \end{align*}$$
When measurement on the first two qubits gives $\ket{00}$, the system is in (not normalized):
$$\ket{\psi’}={1\over2}\ket{00}S\ket\psi+{1\over4}\ket{00}S\ket\psi+{1\over4}\ket{00}XSX\ket\psi$$
$$S= \begin{bmatrix} 1&\\ &i \end{bmatrix},\quad XSX= \begin{bmatrix} i&\\ &1 \end{bmatrix} $$
Assume $\ket\psi=\alpha\ket0+\beta\ket1$, then
$$\begin{align*} \ket{\psi’} & =\ket{00}\left({\frac{3}{4}(\alpha\ket0+i\beta\ket1)+\frac{1}{4}(i\alpha\ket0+\beta\ket1)}\right) \\ & = \ket{00}\left({\left(\frac{3}{4}+\frac{1}{4}i\right)\alpha\ket0+\left(\frac{1}{4}+\frac{3}{4}i\right)\beta\ket1}\right) \end{align*}$$
first remove global phase without normalization
$$\begin{align*} \ket{\psi’} & = \ket{00}\left({\alpha\ket0}+\left({\frac{3}{5}+\frac{4}{5}i}\right)\beta\ket1\right) \end{align*}$$
Which is $$\ket{00}R_z(\theta)\ket\psi$$ with $\cos{\theta}={3/5}$.
ex 4.42
part 1
if $\theta$ is a rational multiple of $2\pi$, assume $$\theta={n\over m}\cdot2\pi$$ where $p$ and $q$ are co-prime, then $$(e^{i\theta})^m=((3+4i)/5)^m=(e^{i{n\over m}2\pi})^m=e^{in2\pi}=1$$ thus we have: $$((3+4i)/5)^m=1$$ $$(3+4i)^m=5^m$$
part 2
$$(3+4i)^2=-7+24i\equiv3+4i\mod 5$$ thus $$(3+4i)^m\equiv3+4i\mod5$$ by induction.
By contradiction, there’s no $m$ can satisfy both. $\theta$ can not be a rational multiple of $2\pi$. $\theta$ is a irrational multiple of $2\pi$
S4.7 Simulation of quantum systems
ex 4.47
$$\begin{align*} e^{i\sum{H_k}t}&=1+i(H_1+\cdots H_k)t-\frac{(H_1+\cdots H_k)^2}{2}t^2-i\frac{(H_1+\cdots H_k)^3}{6}t^3+\cdots\\ &=1+i(H_1+\cdots H_k)t-\frac{\sum{H_k^2}+\sum_{i,j;i\neq j}{(H_iH_j+H_jH_i)}}{2}t^2+\cdots\\ e^{iH_jt}&=1+iH_jt-\frac{H_j^2}{2}t^2-i\frac{H_j^3}{6}t^3+\cdots\\ e^{iH_kt}&=1+iH_kt-\frac{H_k^2}{2}t^2-i\frac{H_k^3}{6}t^3+\cdots \end{align*}$$
Thus:
$$ e^{iH_jt}*e^{iH_kt}=1+i(H_j+H_k)t-\frac{\sum{H_k^2}+2H_jH_k}{2}t^2+\cdots $$
When $e^{iHt}=\prod_k{e^{iH_kt}}$, by comparing the coefficient of $t^2$, we have
$$\begin{align*} H_jH_k+H_kH_j&=2H_jH_k\\ [H_j,H_k]&=0 \end{align*}$$
ex 4.48
Involving at most $c$ particles means that the number of $H_k$ is at most $C_c^n$ which is $O(n^c)$, a polynomial in $n$.
ex 4.49
$e^{(A+B)\Delta t}=1+(A+B)\Delta t+\frac{(A+B)^2}{2}\Delta t^2+O(\Delta t^3)$
$e^{A\Delta t}=1+A\Delta t+{A^2\over2}\Delta t^2+O(\Delta t^3)$
$e^{B\Delta t}=1+B\Delta t+{B^2\over2}\Delta t^2+O(\Delta t^3)$
$e^{-{1\over2}[A,B]\Delta t ^2}=1-{1\over2}[A,B]\Delta t ^2+O(\Delta t^4)$
Thus
$$\begin{align*} e^{A\Delta t}&e^{B\Delta t}e^{-{1\over2}[A,B]\Delta t ^2} \\ &=1+(A+B)\Delta t+(A^2/2+B^2/2+AB-[A,B]/2)+O(\Delta t^3) \\ &=1+(A+B)\Delta t+{1\over2}(A^2+B^2+AB+BA)\Delta t^2+O(\Delta t^3) \\ & =1+(A+B)\Delta t+{(A+B^2)\over2}\Delta t^2+O(\Delta t^3) \end{align*}$$
Hence
$$e^{(A+B)\Delta t}=e^{A\Delta t}e^{B\Delta t}e^{-{1\over2}[A,B]\Delta t ^2}+O(\Delta t^3)$$
ex 4.50
part a.
$$\begin{align*} U_{\Delta t}=1 &-2i(H_1+\cdots H_L)\Delta t\\ &-\left[\left({\sum_{i=1}^n{H_i^2}+2\sum_{i,j,i\neq j}{H_iH_j}}\right)+\sum_{i=1}^n{H_i^2}\right]\Delta t^2+O(\Delta t^3) \\ & = 1-2i(H_1+\cdots H_L)\Delta t-2\left({\sum_{i=1}^n{H_i^2}+\sum_{i,j,i\neq j}{H_iH_j}}\right)\Delta t^2+O(\Delta t^3) \\ & = 1-2iH\Delta t-{(2H)^2\over2!}\Delta t^2 + O(\Delta t^3) \end{align*}$$
Thus
$$U_{\Delta t}-e^{-2iH\Delta t}=O(\Delta t^3)$$
$$U_{\Delta t}=e^{-2iH\Delta t}+O(\Delta t^3)$$
part b.
$$\begin{align*} E(U_{\Delta t}^m,e^{-2miH\Delta t}) & \le mE(U_{\Delta t},e^{-2iH\Delta t}) \\ & = m\cdot O(\Delta t^3)\\ & = m\alpha \Delta t^3 \end{align*}$$
for some $\alpha$.
End of chapter 4
Problem 4.3
(1)
Since $U$ is a unitary, all the eigenvalues have norm equal to $1$.
$$U = \sum_{k=0}^{2^n-1}{e^{-i\theta_k} \ket{k} \bra k}, \quad \theta_k \in[0,2\pi)$$
thus
$$H \equiv i\ln{(U)}=\sum{ \theta_k \ket{k} \bra{k} }$$
(2)
general idea
First, define
$$\mathbf{H}\equiv {H\vert H:2^n\times 2^n \text{ Hermitian}}$$
$$\mathbf{P_n} \equiv {I,X,Y,Z}^{\otimes n}$$
The idea is that $\mathbf{H}$ has $(2^n)^2$ degrees of freedom and $\mathbf{P_n}$ has $4^n = (2^n)^2$ number of elements. Then, if we can prove $\bf{H}$ is a vector space and $\bf{P_n}$ is a basis for $\bf{H}$, then it is obvious that for any $H \in \bf H$ it can be written as $H = \sum_g{h_g g},\quad g\in\bf{P_n}$.
step 1
To prove $\bf{H}$ is a vector space, we can see that $\bf H \subset \bf M$, where $\bf M$ is a vector space which contains all matrices. $\bf H$ is a subspace of $\bf M$. By checking that:
- $\bf 0\in H$
- closure under $+$: for $h_1, h_2\in \bf H$, $(h_1+h_2)^\dagger = h_1^\dagger+h_2^\dagger=(h_1+h_2), (h_1+h_2)\in \bf H$ by definition of Hermitian.
- closure under scalar $*$: $h\in \mathbf{H} \implies ah\in \mathbf H$
$\mathbf H$ is a vector space.
step 2
To prove $\bf{P_n}$ is a basis, fortunately, we can easily prove that all the elements in $\bf{P_n}$ are linearly independent to each other by showing that they are orthogonal.
we use the matrix inner prouct:
$$\left<A,B\right>\equiv tr(A^\dagger B)$$
When $n=1$, which is $$\mathbf{P_1}={I,X,Y,Z}$$, for any two elements $\sigma_1,\sigma_2 \in \mathbf{P_1}$. we can confirm that $\left<\sigma_1,\sigma_2\right>=0$ for $\sigma_1\neq \sigma_2$.
When $n>1$, for $g_1,g_2\in \mathbf{P_n}$ we can write them as: $$\begin{align*} g_1 & =\bigotimes_{i=0}^{n-1}{\sigma_{x_i}},\sigma_{x_i}\in{I,X,Y,Z} \\ g_2 & =\bigotimes_{i=0}^{n-1}{\sigma_{y_i}},\sigma_{y_i}\in{I,X,Y,Z} \end{align*}$$ Then $$\begin{align*} \left<g_1,g_2\right> & = \text{tr}(g_1^{\dagger} g_2) \\ & = \text{tr}\left(\bigotimes_{i=0}^{n-1}{\sigma_{x_i}^\dagger}\bigotimes_{i=0}^{n-1}{\sigma_{y_i}}\right) \\ & = \text{tr}\left(\bigotimes_{i=0}^{n-1}{\sigma_{x_i}^\dagger\sigma_{y_i}}\right) \\ & = \prod_{i=0}^{n-1}{\left<\sigma_{x_i},\sigma_{y_i}\right>} \end{align*}$$
It is clear that, $\left<g_1,g_2\right>\neq0$ only when $\forall i, \sigma_{x_i}=\sigma_{y_i}$, which is $g_1=g_2$. Thus for any two distinctive elements in $\mathbf{P_n}$, their inner product is $0$.
finalizing the proof
Since $\mathbf{H}$ is a vector space with $\text{dim}(\mathbf{H})=\vert{\mathbf{P_n}}\vert=4^n$ , $\mathbf{P_n}\subset\mathbf{H}$ and all the elements in $\mathbf{P_n}$ are orthogonal thus linearly independent, $\mathbf{P_n}$ is a basis for $\mathbf{H}$. For any $H \in \bf H$ it can be written as $H = \sum_g{h_g g},\quad h_g \in \Re, g\in\bf{P_n}$.
(3)
$$\exp{(-ih_gg\Delta)}=\exp{(-i{h_g\over k}\bigotimes_{i=0}^{n-1}{\sigma_{i}})}$$
Based on the method and circuit proposed in section 4.7.3, we replace $\Delta t$ with $h_g/k$. Then for the $i$-th qubit, if $\sigma_i=I$, we remove the $\text{CNOT}$ gates; if $\sigma_i=X$, we add $H$ both before and after the $\text{CNOT}$ gates; if $\sigma_i=Y$, we add $U_3(\pi /2,\pi /2,\pi /2)$ before the $\text{CNOT}$s and $U_3(-\pi /2,\pi /2,\pi /2)$ after the $\text{CNOT}$s; if $\sigma_i=Z$, there should be only $\text{CNOT}$s. There’re at most $4$ gates on a single wire. Thus the construction takes $\text{O}(n)$ number of one and two qubit gates.
(4)
$$\begin{align*} \exp{(-iH\Delta)} & = \exp{(-i\sum_g{h_g g}\Delta)} \end{align*}$$
Using equation $(4.103)$ in chapter 4 and split the summation into $4^n$ terms: $$\exp{(-i\sum_g{h_g g}\Delta)}=\prod_g{}\exp{(-ih_gg\Delta)}+\text{O}(4^n\Delta^2)$$
(5)
Sicne $H \equiv i\ln{(U)}$,
$$\begin{align*} U=e^{-iH} & =\left(\exp{(-iH\Delta)}\right)^k \\ & = \left(\exp{(-i\sum_g{h_g g}\Delta)}\right)^k \\ & = \left(\exp{(-i\sum_g{h_g g}\Delta)}\right)^{k-1}\cdot\prod_g{}\exp{(-ih_gg\Delta)}+\text{O}(4^n\Delta^2) \\ & = \left[\prod_g{}\exp{(-ih_gg\Delta)}\right]^k+k\cdot\text{O}(4^n\Delta^2) \\ & = \left[\prod_g{}\exp{(-ih_gg\Delta)}\right]^k+\text{O}(4^n\Delta) \end{align*}$$
(6)
To be within a distance $\epsilon>0$, $\text{O}(4^n\Delta)<\epsilon$, thus $k=\text{O}(4^n/\epsilon)$. We know that each $\exp{(-ih_gg\Delta)}$ requires $\text{O}{(n)}$ gatesto construct. Hence, $U$ requires $\vert \mathbf{P_n}\equiv{g}\vert\cdot k\cdot\text{O}(n)=\text{O}(n16^n/\epsilon)$